LAB 03.02 - Timeseries model

!wget --no-cache -O init.py -q https://raw.githubusercontent.com/fagonzalezo/ai4eng-unal/main/content/init.py
import init; init.init(force_download=False); init.get_weblink()

from local.lib.rlxmoocapi import submit, session
session.LoginSequence(endpoint=init.endpoint, course_id=init.course_id, lab_id="L03.02", varname="student");

import numpy as np
import matplotlib.pyplot as plt
from local.lib import timeseries as ts
import pandas as pd
import os
from IPython.display import Image
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()
%matplotlib inline

A synthetic timeseries

date_split = "2018-03-01"

idx = pd.date_range("2018-01-01", "2018-03-31", freq="6h")
i = np.linspace(-5,4,len(idx))
i = np.linspace(np.random.random()*5-5,np.random.random()*5+2,len(idx))
t = np.log(i**2+.3)*np.cos(4*i)
t += (np.random.normal(size=len(idx))*.4)
t = np.round(t*3+30,3)
d = pd.DataFrame(np.r_[[t]].T, columns=["signal"], index=idx) 
d.index.name="date"

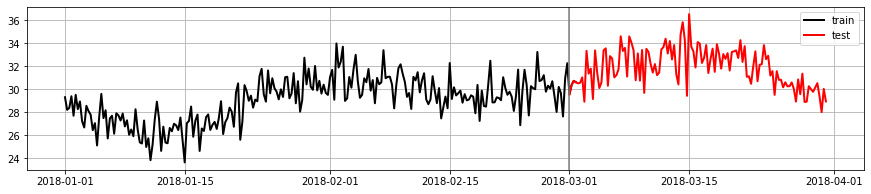
plt.figure(figsize=(15,3))
plt.plot(d[:date_split].index, d[:date_split].signal, color="black", lw="2", label="train"); 
plt.plot(d[date_split:].index, d[date_split:].signal, color="red", lw="2", label="test"); 
plt.axvline(date_split, color="grey"); plt.legend();plt.grid();
signal = d

d.info()

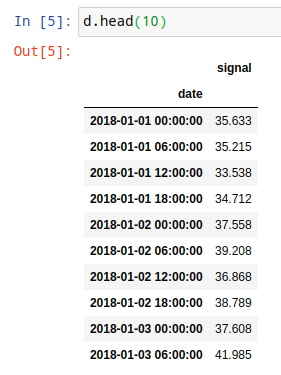
d.head(10)

Task 1. Build a time series training dataset

In this task, starting off from the time signal above, you must build an annotated dataset so that at any time instant given the three last n_timesteps_lookback signal values and the current one we want to predict the next one.

Complete the following function so that when receiving a time indexed dataframe such as the one above, the resulting dataframe is such that:

• the column signal is left untouched

• there are n_timesteps_lookback+1 new columns:

  • the column signal+1 contains the signal one time step into the future

  • the columns signal-1, signal-2, etc. contain the signal one, two, etc. time steps into the past.

• the resulting dataset contains (n_timesteps_lookback+1) rows less than the original dataset, one due to the signal+1 column and the rest for the signal-x columns. For instance, if the original dataset contained 357 rows, with n_timesteps_lookback=3 the resulting dataframe will contain 353 rows.

Hint: use pandas.DataFrame.join, pandas.DataFrame.shift and pandas.DataFrame.dropna

For instance, with this input

Image("local/imgs/df_tseries1.png")

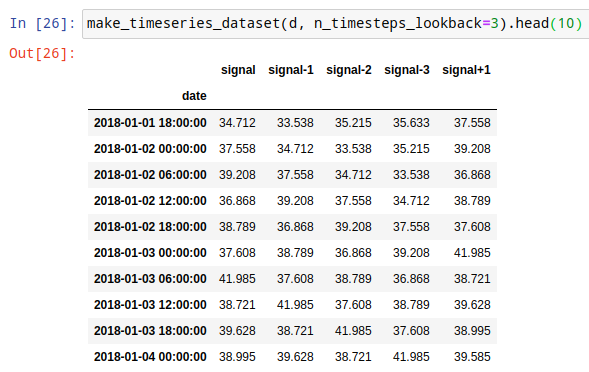
you should produce the following output

Image("local/imgs/df_tseries2.png")

def make_timeseries_dataset(signal, n_timesteps_lookback):
    import pandas as pd
    r = ...
    return r

test your code

make_timeseries_dataset(d, n_timesteps_lookback=3).head(10)

submit your answer

student.submit_task(globals(), task_id="task_01");

Task 2. Manually apply a regression model to create predictions

Complete the following function to apply the a linear regression model to a dataframe such as the resulting one from the previous task:

\[\hat{y} = w_0 + w_1s + w_2s_{-1} + w_3s_{-2} + w_4s_{-3} ... \]

where \(s\) corresponds to the column named signal, \(s_{-1}\) to the column named signal-1, etc.

Observe that:

• column signal+1 is not used, as it is the expected prediction. You will use it in the next task.

• you will have n_timesteps_lookback+2 \(w\) parameters, since you will have one per each n_timesteps_lookback, plus \(w_0\), plus \(w_1\)

Expect the function arguments as follow:

• td: a Pandas dataframe such as the output of the function make_timeseries_dataset of the previous task, with exactly the same column names

• w: a Numpy array with n_timesteps_lookback+2 elements in the order \([w_0, w_1, ...]\)

Warn: the DataFrame td may contain any number of lookback columns and might be in any order

Challenge: solve it with one single line of Python code

EXAMPLE: For the following dataframe and \(w\)

Image("local/imgs/ts_reg_1.png")

you should get the following results

Image("local/imgs/ts_reg_2.png")

def apply_linear_regression_model(td, w):
    r = ... # YOUR SOLUTION HERE
    return r

test your code manually

observe how we permute the columns order

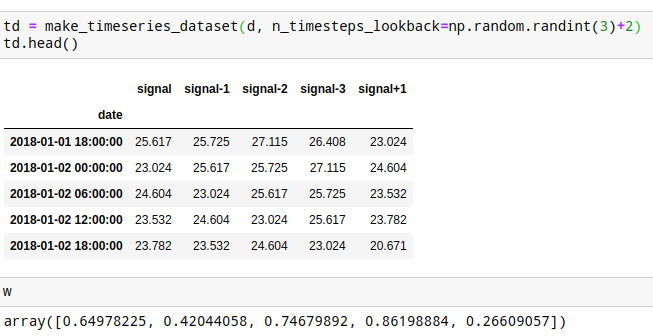
td = make_timeseries_dataset(d, n_timesteps_lookback=np.random.randint(3)+2)
td = td[np.random.permutation(td.columns)]
td.head()

w = np.random.random(len(td.columns))
w

apply_linear_regression_model(td[np.random.permutation(td.columns)], w)[:5]

submit your answer

student.submit_task(globals(), task_id="task_02");

Task 3: Measure trend prediction

You will now use the predictions to measure trend accuracy. We will compare any predictions which are given to us with the actual next value in column signal+1 in the following way

• if signal+1>signal and ALSO your prediction>signal, then your model has a correct trend prediction regardless how different are signal+1 and prediction

• if signal+1<=signal and ALSO your prediction<=signal, then your model has a correct trend prediction regardless how different are signal+1 and prediction

• otherwise, your model has an incorrect prediction

Complete the following function such that when receiving a dataframe such as the resulting one from task 1 above, and a pd.Series with the same index and price predictions, computes the accuracy of the predictions (the percentage of correct predictions).

The accuracy must be a float and its correctness will be checked up to 2 decimal places.

Challenge: solve it with one single line of Python code.

EXAMPLE: for the following time series dataset

Image("local/imgs/ts_reg_3.png")

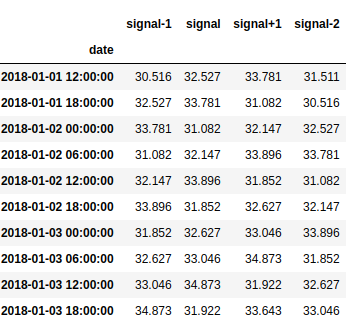
And the following predictions

Image("local/imgs/ts_reg_4.png")

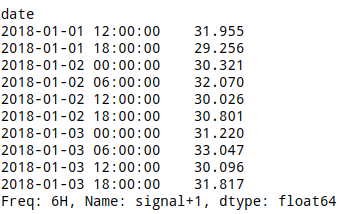
The trend accuracy is 0.4 since the trend is correctly hit by the predictions on rows 1, 4, 7 and 8 (assuming the first row is numbered as 0)

def measure_trend_accuracy(td, preds):
    r = ... # YOUR CODE HERE
    return r

test your code manually

td = make_timeseries_dataset(d, n_timesteps_lookback=np.random.randint(3)+2).iloc[:10]
td

preds = td['signal'] + np.round(np.random.random()*4-2,3)
preds

measure_trend_accuracy(td, preds)

submit your answer

student.submit_task(globals(), task_id="task_03");