07.04 - TENSORFLOW#
!wget --no-cache -O init.py -q https://raw.githubusercontent.com/fagonzalezo/ai4eng-unal/main/content/init.py
import init; init.init(force_download=False); init.get_weblink()
endpoint https://m5knaekxo6.execute-api.us-west-2.amazonaws.com/dev-v0001/rlxmooc
import numpy as np
import matplotlib.pyplot as plt
from local.lib import mlutils
from IPython.display import Image
try:
%tensorflow_version 2.x
print ("Using TF2 in Google Colab")
except:
pass
import tensorflow as tf
%matplotlib inline
A dataset (again)#
## KEEPOUTPUT
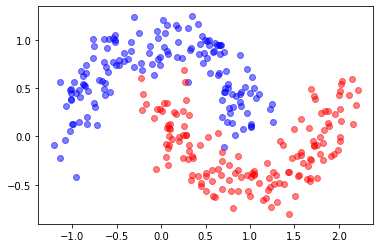
from sklearn.datasets import make_moons
X,y = make_moons(300, noise=.15)
plt.scatter(X[:,0][y==0], X[:,1][y==0], color="blue", label="class 0", alpha=.5)
plt.scatter(X[:,0][y==1], X[:,1][y==1], color="red", label="class 1", alpha=.5)
<matplotlib.collections.PathCollection at 0x7f34b2988f70>
A bigger network#
different activation functions
different optimizer
model = tf.keras.Sequential([
tf.keras.layers.Dense(20, activation='tanh'),
tf.keras.layers.Dense(50, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid')
])
model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=.01),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=False),metrics=['accuracy'])
## KEEPOUTPUT
model.fit(X,y, epochs=10, batch_size=1)
Epoch 1/10
300/300 [==============================] - 0s 510us/step - loss: 0.3400 - accuracy: 0.8567
Epoch 2/10
300/300 [==============================] - 0s 508us/step - loss: 0.2804 - accuracy: 0.8867
Epoch 3/10
300/300 [==============================] - 0s 487us/step - loss: 0.2450 - accuracy: 0.8967
Epoch 4/10
300/300 [==============================] - 0s 532us/step - loss: 0.1722 - accuracy: 0.9433
Epoch 5/10
300/300 [==============================] - 0s 516us/step - loss: 0.1660 - accuracy: 0.9500
Epoch 6/10
300/300 [==============================] - 0s 527us/step - loss: 0.0917 - accuracy: 0.9700
Epoch 7/10
300/300 [==============================] - 0s 516us/step - loss: 0.1127 - accuracy: 0.9667
Epoch 8/10
300/300 [==============================] - 0s 507us/step - loss: 0.1118 - accuracy: 0.9600
Epoch 9/10
300/300 [==============================] - 0s 526us/step - loss: 0.1076 - accuracy: 0.9500
Epoch 10/10
300/300 [==============================] - 0s 487us/step - loss: 0.0840 - accuracy: 0.9800
<tensorflow.python.keras.callbacks.History at 0x7f340807ac10>
## KEEPOUTPUT
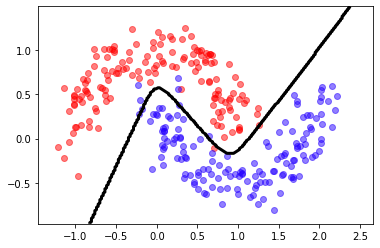
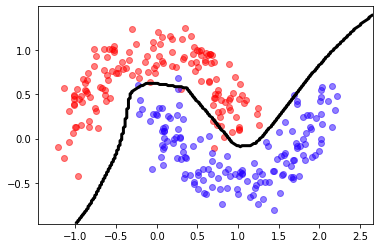
predict = lambda X: (model.predict(X)[:,0]>.5).astype(int)
mlutils.plot_2Ddata_with_boundary(predict, X, y)
(0.522575, 0.477425)
Cross entropy - multiclass classification#
follow THIS EXAMPLE in TensorFlow doc site. Observe that:
labels corresponding to a 10-class classification problem
the network contains 10 output neurons, one per output class
the loss function is
SparseCategoricalCrossEntropy
Observe how cross entropy works with 4 classes:
first we convert the output to a one-hot encoding
we create a network with two output neurons with sigmoid activation
interpret each neuron’s output as elements of a probability distribution
normalize the probability distribution (must add up to one)
we consider network output is better when it yields more probability to the correct class
expected classes for five data points
## KEEPOUTPUT
y = np.random.randint(4, size=5)
y
array([3, 1, 2, 0, 3])
convert it to one hot encoding
## KEEPOUTPUT
y_ohe = np.eye(4)[y].astype(int)
y_ohe
array([[0, 0, 0, 1],
[0, 1, 0, 0],
[0, 0, 1, 0],
[1, 0, 0, 0],
[0, 0, 0, 1]])
simulate some neural network output with NO ACTIVATION function
with 10 output neurons, so for each input element (we have five) we have 4 outputs.
this is called LOGITS in Tensorflow
## KEEPOUTPUT
y_hat = np.round(np.random.normal(size=y_ohe.shape), 2)
y_hat
array([[ 0.06, -0.31, -0.95, 0.39],
[ 0.92, -0.48, -0.08, 0.53],
[-0.5 , 0.22, -0.18, 1.81],
[-0.49, -1.41, 0.09, -0.11],
[-0.73, 0.26, -1.63, -0.68]])
normalize LOGITS. This is the SOFTMAX function
LOGITS obtained from network last layer with no activation
SOFTMAX ACTIVATION
with
this ensures:
\(\sum_{k=0}^9 \hat{\bar{y}}^{(i)}_k=1\)
\(0 \le \hat{\bar{y}}^{(i)}_k \le 1\)
this way, for each input we have a nice probability distribution in its outputs.
This is implemented in Tensorflow
## KEEPOUTPUT
y_hatb = tf.nn.softmax(y_hat).numpy()
y_hatb
array([[0.29019814, 0.20044982, 0.10569567, 0.40365637],
[0.43638904, 0.10761221, 0.16053855, 0.2954602 ],
[0.06893706, 0.14162659, 0.09493514, 0.69450122],
[0.21519991, 0.08576126, 0.38435531, 0.31468351],
[0.19420963, 0.52266365, 0.07895974, 0.20416697]])
check sums
## KEEPOUTPUT
y_hatb.sum(axis=1)
array([1., 1., 1., 1., 1.])
how would you now measure how closely y_hatb is to the expected output on y_ohe?
cross entropy: just take the probability assigned to the correct class (and pass it through a log function)
where \(\bar{\mathbf{y}}^{(i)}\) is the one-hot encoding of the expected class (label) for data point \(i\).
observe that,
in the one-hot encoding \(\bar{\mathbf{y}}^{(i)}\) only one of the elements will be 1, and the rest will be 0’s, so the sumation above is only taking the log of the probability of the correct label.
the negative sign accounts for logs of values <1 are negative and we will later want to minimize the loss
This is implemented in Tensorflow
## KEEPOUTPUT
tf.keras.losses.categorical_crossentropy(y_ohe, y_hatb)
<tf.Tensor: shape=(5,), dtype=float64, numpy=array([0.90719134, 2.22922115, 2.35456137, 1.53618786, 1.58881713])>
Observe that TensorFlow also implements the corresponding sparse convenience function that works directly with our labels
## KEEPOUTPUT
tf.keras.losses.sparse_categorical_crossentropy(y, y_hatb)
<tf.Tensor: shape=(5,), dtype=float64, numpy=array([0.90719134, 2.22922115, 2.35456137, 1.53618786, 1.58881713])>