LAB 07.02 - Neural networks#
!wget --no-cache -O init.py -q https://raw.githubusercontent.com/fagonzalezo/ai4eng-unal/main/content/init.py
import init; init.init(force_download=False); init.get_weblink()
from local.lib.rlxmoocapi import submit, session
session.LoginSequence(endpoint=init.endpoint, course_id=init.course_id, lab_id="L07.02", varname="student");
import numpy as np
from IPython.display import Image
try:
%tensorflow_version 2.x
print ("Using TF2 in Google Colab")
except:
pass
import tensorflow as tf
Task 1. Compute softmax output#
You have a classification problem with \(n_c\) classes. You have a dataset of \(m\) elements and you are given:
\(\hat{\mathbf{y}} \in \mathbb{R}^{m\times n_c}\), the logits of the output layer of a neural network
compute \(\hat{\bar{\mathbf{y}}}\) the softmax output corresponding the given logits, as explained in the notes.
NOTE: You will not be able to use tensorflow in your solution. The grader will penalize you if you do.
CHALLENGE: Use a single line of Python code
def softmax(y_hat):
return ... # YOUR CODE HERE
check your code against Tensorflow. Your answer must be exactly the same
m = np.random.randint(10)+10
nc = np.random.randint(5)+5
y_hat = np.round(np.random.normal(size=(m,nc)), 2)
y_hat
array([[-0.84, -0.29, 0.66, 1.14, 1.31, 0.88, -0.2 ],
[-0.69, 0.05, 1.68, -0.62, 0.31, -0.13, -0.68],
[-1.47, -0.37, -1.86, -0.15, 1.12, -0.59, -0.4 ],
[ 0.98, -0.53, 1.33, 0.32, -0.85, -0.05, -0.63],
[-1.39, -0.12, -1.44, 0.12, 1.2 , -0.23, -0.11],
[-1.23, 0.1 , -0.07, -1.47, 0.88, 0.04, 0.53],
[-0.59, -0.83, -1.23, -1.05, 0.45, 0.12, 1.62],
[-1.02, -0.17, -0.41, -2.29, -1.17, 0.25, -1.32],
[-0.48, -2.1 , 2.4 , -0.21, 0.51, -0.42, 0.75],
[-1.03, -0.53, -2.42, 0.5 , -0.48, -0.71, 0.25],
[-1.89, -1.79, 0.38, -0.44, -0.3 , 0.29, -2.53],
[ 0.84, 0.26, -0.03, -1.89, 2.42, 0.04, -0.11]])
my_output = softmax(y_hat)
my_output
tf_output = tf.nn.softmax(y_hat).numpy()
tf_output
np.allclose(my_output, my_output)
submit your code
student.submit_task(globals(), task_id="task_01");
Task 2: Compute cross entropy#
you are also given
\(\mathbf{y}\), a vector of \(m\) elements, each elemet being an integer between \(0\) and \(n_c-1\), corresponding to the labels of your dataset.
Complete the following function to compute cross entropy as explained in the notes. Observe that you are given:
\(\mathbf{y}\) with the original class labels. You will have to convert it to a one hot encoding.
\(\hat{\bar{\mathbf{y}}}\) the softmax activations such as from the output on your previous function
NOTE: You will not be able to use tensorflow in your solution. The grader will penalize you if you do.
SUGGESTION: Use np.log(expression+1e-10) for any expression better than np.log(expression) since this will avoid numeric errors if expression evaluates to 0. Recall that 1e-10 is \(10^{-10}\)
CHALLENGE: Use a single line of Python code
def cross_entropy(y, y_hatb):
return ... # YOUR CODE HERE
check your answer against Tensorflow corresponding implementation
m = np.random.randint(10)+10
nc = np.random.randint(5)+5
y = np.random.randint(nc, size=m)
y_hatb = np.random.random(size=(m, nc))
y_hatb /= np.sum(y_hatb, axis=1).reshape(-1,1)
print (y)
print (y_hatb)
print (y_hatb.sum(axis=1))
cross_entropy(y, y_hatb)
tf.keras.losses.sparse_categorical_crossentropy(y, y_hatb).numpy()
submit your code
student.submit_task(globals(), task_id="task_02");
Task 3: Compute multilayer perceptron network output#
You have
a dataset of \(m\) elements and \(n\) columns.
a classification problem with \(n_c\) classes.
And we build a multilayer perceptron with
two hidden layers with \(h_1\) and \(h_2\) neurons respectively and tanh activation.
one output layer with \(n_c\) neurons with softmax activation.
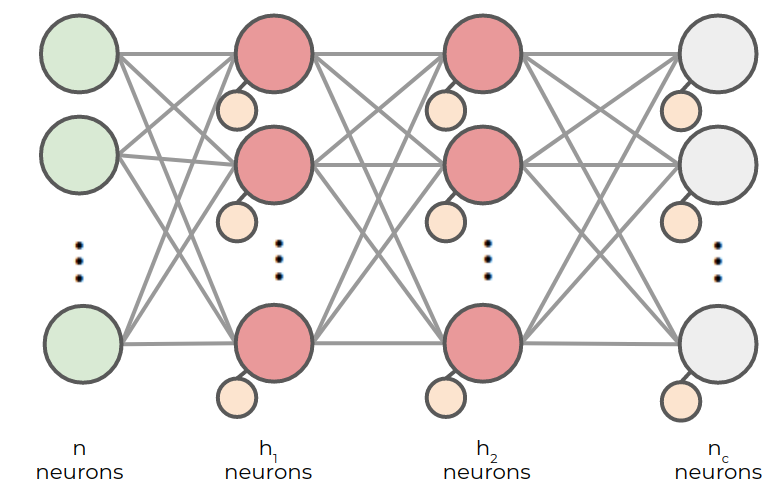
so that we have the following architecture
This way, we have the following set of weights:
\(W_0 \in \mathbb{R}^{n\times h_1}\)
\(b_0 \in \mathbb{R}^{h_1}\)
\(W_1 \in \mathbb{R}^{h1\times h_2}\)
\(b_1 \in \mathbb{R}^{h_2}\)
\(W_2 \in \mathbb{R}^{h2\times n_c}\)
\(b_2 \in \mathbb{R}^{n_c}\)
Complete the function below so that it produces the following output:
NOTE: You will not be able to use tensorflow in your solution. The grader will penalize you if you do.
CHALLENGE: Use a single line of Python code (not counting your previous softmax function).
def nn_output(X, W0, b0, W1, b1, W2, b2):
def softmax .... # use your softmax from task above
return ... # YOUR CODE HERE
check your code with random input and weights against the implementation in Tensorflow
m = np.random.randint(10)+10
n = np.random.randint(3)+3
nc = np.random.randint(5)+5
m = 10
n = 3
nc = 4
h1 = np.random.randint(5)+5
h2 = np.random.randint(5)+5
print (m,n,nc)
X = np.random.normal(size=(m,n))
W0 = np.random.normal(size=(n,h1))
b0 = np.random.normal(size=h1)
W1 = np.random.normal(size=(h1,h2))
b1 = np.random.normal(size=h2)
W2 = np.random.normal(size=(h2,nc))
b2 = np.random.normal(size=nc)
your function output
nn_output(X, W0, b0, W1, b1, W2, b2)
model = tf.keras.Sequential([
tf.keras.layers.Dense(h1, activation='tanh', dtype=tf.float64),
tf.keras.layers.Dense(h2, activation='tanh', dtype=tf.float64),
tf.keras.layers.Dense(nc, activation='softmax', dtype=tf.float64)
])
model.build(input_shape=[None, n])
model.set_weights([W0, b0, W1, b1, W2, b2])
tensorflow output (must be exactly as yours)
model(X).numpy()
submit your code
student.submit_task(globals(), task_id="task_03");