1.2 - Models derived from data

!wget -nc --no-cache -O init.py -q https://raw.githubusercontent.com/rramosp/2021.deeplearning/main/content/init.py
import init; init.init(force_download=False); 

¿Qué es Machine Learning (ML)?

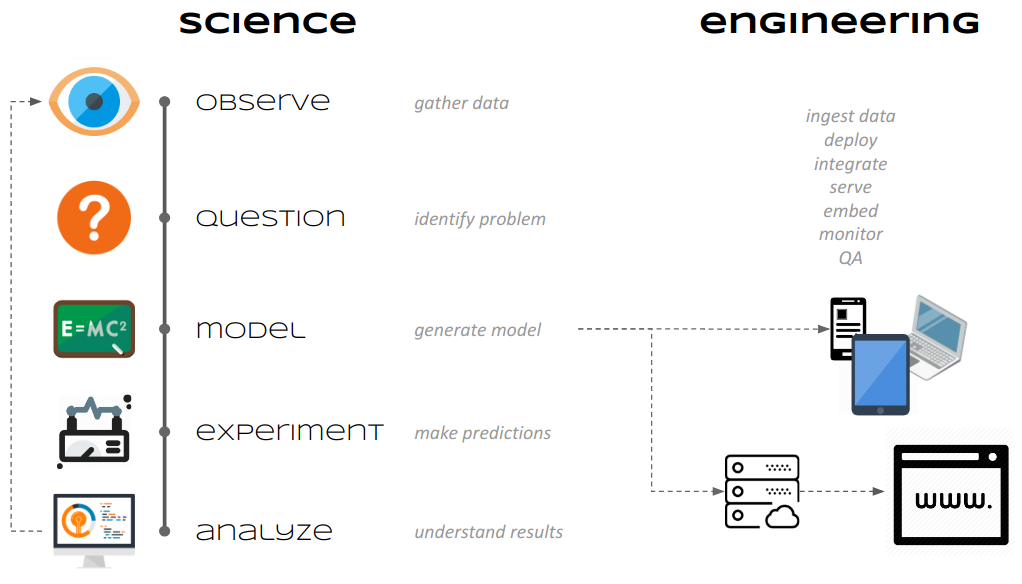
Primero realizamos experimentos (ciencia), después desarrollamos productos (ingeniería)

Dos roles \(\rightarrow\) dos flujos de trabajo:

• diseñador de algoritmos de ML \(\rightarrow\) se enfoca en cómo se genera un modelo.

• usuario de algoritmos de ML \(\rightarrow\) se enfoca que calibrar modelos respecto a unos datos concretos.

from IPython.display import Image
Image(filename='local/imgs/science_engineering.png', width=600)

Image(filename='local/imgs/ml_workflows_tools.png', width=600)

¿Qué es un modelo derivado de los datos?

Caso ideal: Sabemos las distribuciones de las que vienen los datos. \(\Rightarrow\) podemos calcular analíticamente nuestro modelo.

• ¿Podemos encontrar un modelo con 100% de acierto? ¿Por qué sí, o por qué no?

from scipy import stats
from scipy import optimize
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

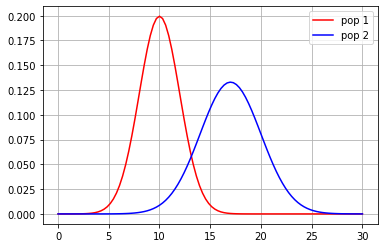
d1 = stats.norm(loc=10,scale=2)
d2 = stats.norm(loc=17,scale=3)


x = np.linspace(0,30,100)
plt.plot(x, d1.pdf(x), color="red", label="pop 1")
plt.plot(x, d2.pdf(x), color="blue", label="pop 2")
plt.grid()
plt.legend();

x = np.linspace(5,25,1000)
minx = x[np.argmin(np.abs(d1.pdf(x)-d2.pdf(x)))]

print("frontera óptima en %.2f"%minx)

x = np.linspace(0,30,100)
plt.plot(x, d1.pdf(x), color="red", label="pop 1")
plt.plot(x, d2.pdf(x), color="blue", label="pop 2")
plt.axvline(minx, color="black", label="óptimo = %.2f"%minx)
plt.grid()
plt.legend();

frontera óptima en 13.15

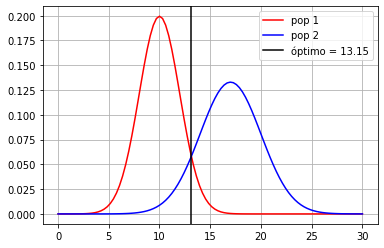
cálculo analítico de los errores de clasificación

print("pop 1 error", 1-d1.cdf(minx))
print("pop 2 error", d2.cdf(minx))

pop 1 error 0.05773516274534907
pop 2 error 0.09957961739117976

Caso real: Tenemos una muestra de los datos

\(\rightarrow\) ¿Cómo determinamos donde poner la frontera?

\(\rightarrow\) ¿Qué frontera qusiéramos obtener?

def show_1D_dataset_samples(n, n_datasets=10, dot_alpha=.5, line_alpha=.5, figsize=(20,5)):
    from sklearn.tree import DecisionTreeClassifier
    plt.figure(figsize=figsize)
    for i in range(n_datasets):

        m1 = d1.rvs(n)
        m2 = d2.rvs(n)
        X = np.append(m1, m2).reshape(-1,1)
        y = np.r_[[0]*len(m1)+[1]*len(m2)]
        estimator = DecisionTreeClassifier(max_depth=1)
        estimator.fit(X,y)
        Xr = np.linspace(5, 30, 100).reshape(-1,1)
        yr = estimator.predict(Xr)
        plt.plot(Xr[yr==0], [i]*np.sum(yr==0), color="red", alpha=line_alpha, lw=4)
        plt.plot(Xr[yr==1], [i]*np.sum(yr==1), color="blue", alpha=line_alpha, lw=4)
        plt.scatter(m1, [i+.1]*len(m1), color="red", alpha=dot_alpha, s=100)
        plt.scatter(m2, [i+.1]*len(m2), color="blue", alpha=dot_alpha, s=100)
    plt.axis("off")

show_1D_dataset_samples(10, n_datasets=1, dot_alpha=.5, line_alpha=0, figsize=(20,1))
plt.axis("on")
plt.ylim(.095, .105)
plt.yticks([])
plt.axhline(.1, color="black", alpha=.2)

<matplotlib.lines.Line2D at 0x7f6f68cd1790>

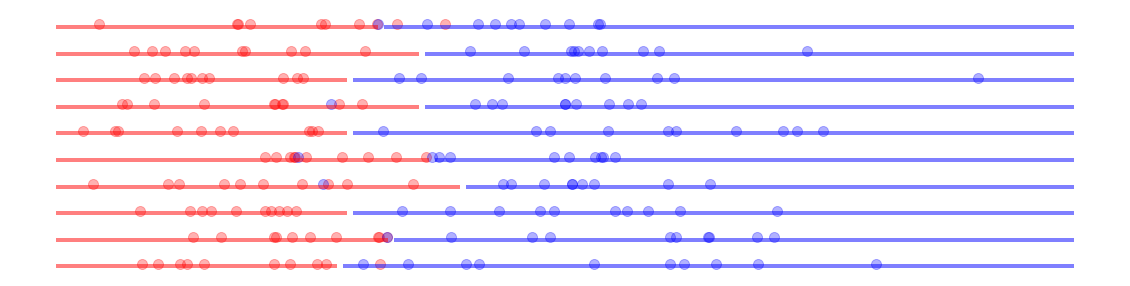
show_1D_dataset_samples(10, dot_alpha=.3)

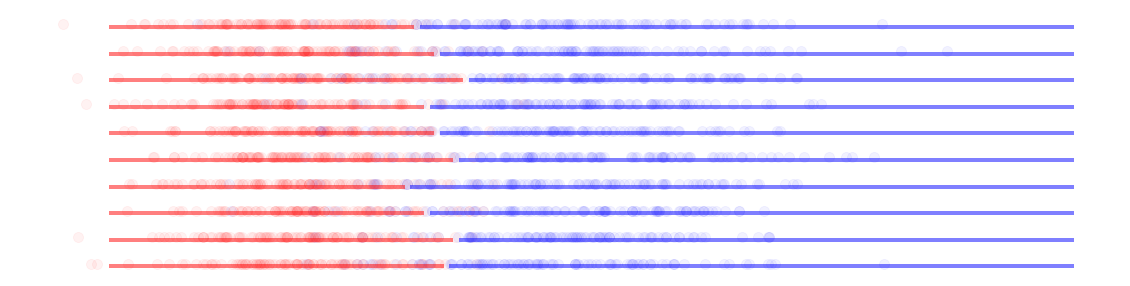
show_1D_dataset_samples(100, dot_alpha=.05)

show_1D_dataset_samples(10000, dot_alpha=.001)

Caso en 2D

• en 2D, un modelo de clasificación es una frontera en el plano

• supongamos que tenemos acceso a las distribuciones de las que surgen los datos \(\rightarrow\) podemos muestrear tantas veces como queramos

• ¿cuál es la frontera que produce menos error de clasificación?

• \(\epsilon\) es el error de clasificación calculado analíticamente con la frontera óptima porque conocemos las distribuciones que generan los datos.

• \(\hat{\epsilon}\) es el error de clasificacón calculado con la muestra de datos y con la frontera óptima (conocida también como frontera bayesiana).

from local.lib import mlutils
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC

%matplotlib inline

mc = mlutils.Example_Bayes2DClassifier(mean0=[1.5, 2.5], cov0=[[0.1, 0.], [0., 0.1]],
                                        mean1=[1.5, 2.], cov1=[[0.2,0.1],[0,.2]])
X,y = mc.sample(500)
mlutils.plot_2Ddata_with_boundary(mc.predict, X, y, line_width=3, line_color="green", dots_alpha=.3)
plt.title(" $\hat{\epsilon}=%.3f$"%mc.score(X,y)+"  $\epsilon=%.3f$"%mc.analytic_score());
plt.grid();

/opt/anaconda/lib/python3.7/site-packages/scipy/stats/_multivariate.py:660: RuntimeWarning: covariance is not symmetric positive-semidefinite.
  out = random_state.multivariate_normal(mean, cov, size)

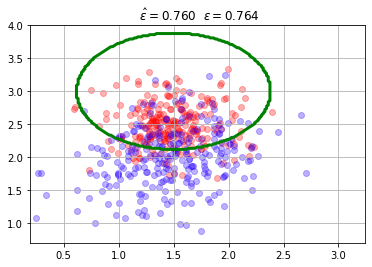
haz los siguientes experimentos:

• separa los centros de las distribuciones de cada clase (mean0, mean1).

• aumenta y disminuye las matrices de covarianza.

• aumenta y disminuye el número de muestras.

• observa la estabilidad de \(\hat{\epsilon}\) respecto a \(\epsilon\) según ambas clases están más mezcladas o hay más o menos datos.

en general SOLO TENEMOS UNA MUESTRA de los datos, porque no tenemos conocimiento de las distribuciones que los generan. Los métodos de estadística y de machine learning están diseñados para esta situación.

Ejecuta la siguiente celda y pregúntate cada vez, ¿qué frontera establecerías con los datos que ves?.

Fíjate que tenemos distintas muestras de una misma disitribución de base. Es decir, la realidad detrás de estos datos siempre es la misma.

Aumenta el número de muestras y hazte cada vez la misma pregunta.

X,y = mc.sample(30)
mlutils.plot_2Ddata(X, y, dots_alpha=.3)
plt.grid()

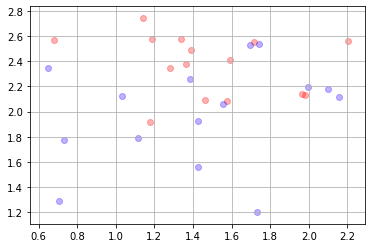
Los algoritmos de machine learning:

• Los algoritmos de clasificación calculan fronteras entre los datos.

• Parten de una muestra de los datos, no de las distribuciones.

• Por tanto, no conocemos la forma de la frontera bayesiana.

O sea, partimos ciegos!!!!!!!

Para abordar esta situación, cualquier algoritmo tiene necesariamente que plantear una alguna suposición de base:

• los datos vienen de distribuciones normales.

• las columnas son estadísticamente independientes.

• la frontera es lineal, o cuadrática.

• la frontera se representa con una red neuronal.

Teniendo esto en cuenta, y partiendo de una muestra de los datos:

• el objetivo de un usuario de ML es acercarse lo más posible a la frontera bayesiana (que no sabemos cómo es).

• distintos algoritmos ML tienen distintas capacidades para modelar fronteras (un clasificador lineal no puede captuarar una frontera cuadrática).

• necesitamos dos tipos de herramientas:

  • una buena colección de algoritmos ML.

  • métodos para saber qué tan cerca estamos de la frontera bayesiana.

observa cómo un clasificador lineal aproxima la frontera con diferentes tamaños de muestras

• cambia el parámetro n_samples y experimenta con el siguiente código.

• usa luego estimadores distintos. P.ej.

    estimator = SVC(gamma=1)
    estimator = RandomForestClassifier()
    estimator = SVC(gamma=100)
  

Hazte las siguientes preguntas:

• ¿qué complejidad es capaz de capturar un estimador?

from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
import importlib
importlib.reload(mlutils)
n_samples = 50
estimator = LogisticRegression()
estimator = SVC(gamma=.5)
plt.figure(figsize=(15,3))
for i in range(3):
    plt.subplot(1,3,i+1)
    mlutils.plot_estimator_border(mc, estimator, mins=[0,-1], maxs=[3,4], n_samples=n_samples, legend=False)

/opt/anaconda/lib/python3.7/site-packages/scipy/stats/_multivariate.py:660: RuntimeWarning: covariance is not symmetric positive-semidefinite.
  out = random_state.multivariate_normal(mean, cov, size)
/opt/anaconda/lib/python3.7/site-packages/scipy/stats/_multivariate.py:660: RuntimeWarning: covariance is not symmetric positive-semidefinite.
  out = random_state.multivariate_normal(mean, cov, size)

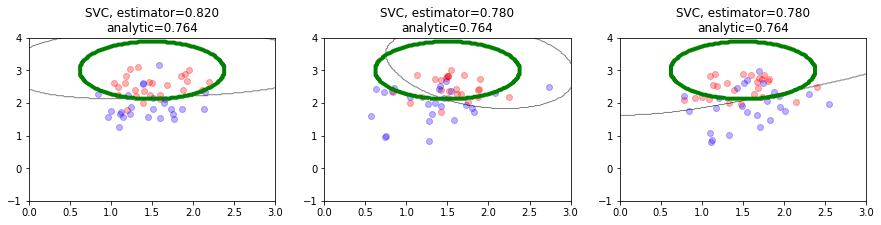
hacemos ahora el experimento más exhaustivo repitiendo 20 veces el siguiente proceso:

• se muestrea el dataset (recuerda que excepcionalmente tenemos acceso a las distribuciones que generan los datos y por tanto podemos hacer esto).

• se calcula la fronter de clasificación obtenida por el estimador usando el dataset muestreado.

• se pinta esta frontera (en negro).

• en verde se muestra la frontera bayesiana.

import importlib
import warnings
warnings.filterwarnings("ignore")
importlib.reload(mlutils)
mlutils.sample_borders(mc, estimator, samples = [10,50,100,500], n_reps=20, mins=[0,-1], maxs=[3,4])

100% (4 of 4) |##########################| Elapsed Time: 0:00:05 Time:  0:00:05

Solo tenemos un dataset

• remuestrea, reentrena para medir el desempeño y entender la estabilidad

• prueba con test_pct entre 0.1 y 0.9. observa la divergencia entre train y test cuando test_pct es más cercano a 0.9. ¿por qué?

• prueba con SVC(gamma=100). En este caso observa la divergencia entre train y test incluso cuando test_pct es pequeño. ¿por qué?

• prubea además con dataset_size entre 20 y 500

Entiende la diferencia entre tener pocos datos y overfitting

Configuraciones interesantes sobre

mc = mlutils.Example_Bayes2DClassifier(mean0=[1.5, 1.5], cov0=[[0.5, 0.1], [0.3, 0.5]],
                                        mean1=[1.2, 2.], cov1=[[0.2,0.1],[0,.5]])

• SVC \(\gamma=100\), dataset_size=500 (overfitting con pocos datos, convergencia con muchos)

• SVC \(\gamma=100\), dataset_size=2000 (overfitting con pocos datos, convergencia con muchos)

• SVC \(\gamma=.01\), dataset_size=100 (variabilidad siempre, convergencia promedio con pocos datos)

• SVC \(\gamma=1\), dataset_size=100 (variabilidad siempre, convergencia promedio con pocos datos)

• LinearRegression, dataset_size=100 (nunca converge a la frontera bayesiana)

from local.lib import mlutils
dataset_size = 200
mc = mlutils.Example_Bayes2DClassifier(mean0=[1.5, 1.5], cov0=[[4., 0.5], [0.1, 4.]],
                                        mean1=[1.5,4.], cov1=[[1,0.5],[0.1,1.]])
X,y = mc.sample(dataset_size)
mlutils.plot_estimator_border(mc, n_samples=dataset_size, legend=False)
analitic_score = mc.analytic_score()

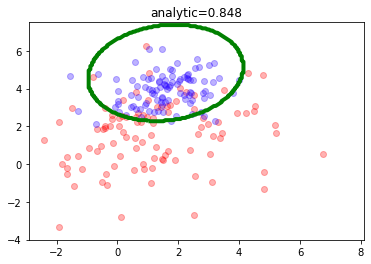
realizamos un muestreo para dividir entre train y test

test_pct = .3
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=test_pct)
print(X_train.shape, y_train.shape)
print(X_test.shape, y_test.shape)

(140, 2) (140,)
(60, 2) (60,)

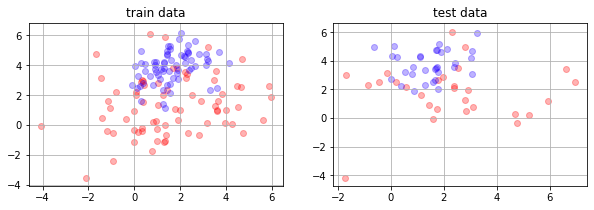
plt.figure(figsize=(10,3))
plt.subplot(121)
mlutils.plot_2Ddata(X_train, y_train, dots_alpha=.3)
plt.title("train data")
plt.grid()
plt.subplot(122)
mlutils.plot_2Ddata(X_test, y_test, dots_alpha=.3)
plt.grid()
plt.title("test data")

Text(0.5, 1.0, 'test data')

#estimator = SVC(gamma=1)
estimator = SVC(gamma=100)
#estimator = LogisticRegression()
#estimator = RandomForestClassifier()
estimator.fit(X_train, y_train)

SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
    decision_function_shape='ovr', degree=3, gamma=100, kernel='rbf',
    max_iter=-1, probability=False, random_state=None, shrinking=True,
    tol=0.001, verbose=False)

print("accuracy train %.2f"%estimator.score(X_train,y_train))
tr_preds = estimator.predict(X_train)
print("predicciones para train")
print(tr_preds)
print("ground truth para train")
print(y_train)

print("\naccuracy test %.2f"%estimator.score(X_test,y_test))
ts_preds = estimator.predict(X_test)
print("predicciones para test")
print(ts_preds)
print("ground truth para test")
print(y_test)

accuracy train 1.00
predicciones para train
[1. 1. 1. 0. 0. 1. 0. 1. 0. 1. 1. 1. 0. 1. 1. 0. 0. 0. 0. 0. 0. 0. 0. 1.
 1. 1. 1. 1. 0. 0. 1. 1. 1. 1. 1. 0. 1. 1. 0. 1. 1. 0. 0. 0. 0. 1. 1. 0.
 1. 1. 1. 1. 0. 1. 0. 0. 1. 1. 0. 1. 1. 0. 0. 1. 1. 1. 0. 1. 1. 0. 1. 0.
 0. 0. 1. 0. 0. 0. 1. 0. 0. 1. 1. 0. 1. 1. 1. 0. 0. 0. 0. 0. 0. 1. 0. 1.
 0. 0. 0. 1. 0. 0. 0. 0. 1. 0. 1. 1. 0. 1. 0. 0. 1. 0. 1. 0. 0. 0. 1. 0.
 0. 0. 1. 1. 1. 0. 0. 1. 0. 1. 0. 0. 1. 1. 0. 1. 0. 1. 1. 0.]
ground truth para train
[1. 1. 1. 0. 0. 1. 0. 1. 0. 1. 1. 1. 0. 1. 1. 0. 0. 0. 0. 0. 0. 0. 0. 1.
 1. 1. 1. 1. 0. 0. 1. 1. 1. 1. 1. 0. 1. 1. 0. 1. 1. 0. 0. 0. 0. 1. 1. 0.
 1. 1. 1. 1. 0. 1. 0. 0. 1. 1. 0. 1. 1. 0. 0. 1. 1. 1. 0. 1. 1. 0. 1. 0.
 0. 0. 1. 0. 0. 0. 1. 0. 0. 1. 1. 0. 1. 1. 1. 0. 0. 0. 0. 0. 0. 1. 0. 1.
 0. 0. 0. 1. 0. 0. 0. 0. 1. 0. 1. 1. 0. 1. 0. 0. 1. 0. 1. 0. 0. 0. 1. 0.
 0. 0. 1. 1. 1. 0. 0. 1. 0. 1. 0. 0. 1. 1. 0. 1. 0. 1. 1. 0.]

accuracy test 0.60
predicciones para test
[1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 1.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 1. 0. 0. 1. 1. 1. 0.
 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
ground truth para test
[1. 0. 0. 0. 0. 0. 1. 0. 1. 0. 0. 1. 0. 1. 0. 1. 1. 0. 0. 0. 0. 0. 1. 1.
 1. 1. 0. 0. 0. 0. 1. 1. 1. 0. 1. 0. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1. 0. 0.
 1. 0. 0. 1. 0. 1. 1. 1. 1. 1. 0. 1.]

np.min(X, axis=0)

array([-4.07714226, -4.20674506])

X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=test_pct)
estimator.fit(X_train, y_train)
trsc = estimator.score(X_train, y_train)
tssc = estimator.score(X_test, y_test)
print("train_score %5.2f"%estimator.score(X_train, y_train))
print("test_score  %5.2f"%estimator.score(X_test, y_test))

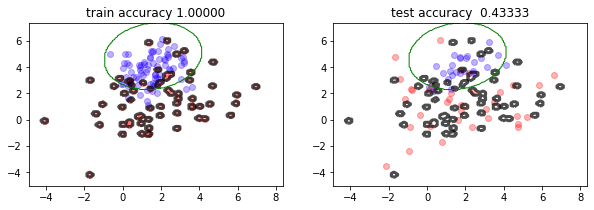
plt.figure(figsize=(10,3))
plt.subplot(121)
mlutils.plot_2Ddata(X_train, y_train, dots_alpha=.3)
mlutils.plot_2D_boundary(estimator.predict, np.min(X, axis=0), np.max(X, axis=0),
                 line_width=3, line_alpha=.7, label=None)
plt.title("train accuracy %.5f"%estimator.score(X_train, y_train))

mlutils.plot_2D_boundary(mc.predict, np.min(X, axis=0), np.max(X, axis=0),
                 line_width=1, line_alpha=1., line_color="green", label="bayes boundary")

plt.subplot(122)
mlutils.plot_2Ddata(X_test, y_test, dots_alpha=.3)
mlutils.plot_2D_boundary(estimator.predict, np.min(X, axis=0), np.max(X, axis=0),
                 line_width=3, line_alpha=.7, label=None)
plt.title("test accuracy  %.5f"%estimator.score(X_test, y_test))
mlutils.plot_2D_boundary(mc.predict, np.min(X, axis=0), np.max(X, axis=0),
                 line_width=1, line_alpha=1., line_color="green", label="bayes boundary")

train_score  1.00
test_score   0.43

(0.878175, 0.121825)

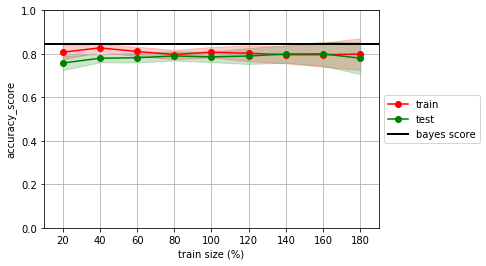
Multidimensionalidad (>2D)

normalmente tenemos datasets de muchas dimensiones (columnas) y no podemos visualizar los datos como en 2D \(\rightarrow\) necesitamos métodos para recabar evidencia sobre si tenemos pocos datos, estamos haciendo overfitting, etc.

Las curvas de aprendizaje nos ayudan a esto.

Realiza el experimento desde la sección anterior, con distintos tamaños del dataset inicial y con distintos algoritmos.

estimator = LogisticRegression()
mlutils.lcurve(estimator, X, y, n_reps=20, score_func=accuracy_score)
plt.axhline(analitic_score, lw=2, color="black", label="bayes score")
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))

100% (9 of 9) |##########################| Elapsed Time: 0:00:00 Time:  0:00:00

<matplotlib.legend.Legend at 0x7fbdb9f5d198>

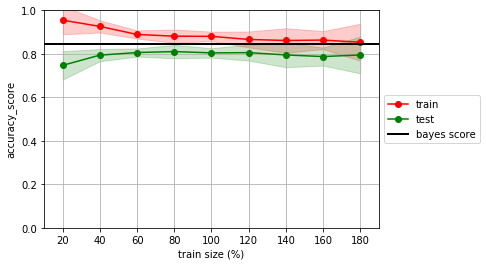
estimator = SVC(gamma=1)
mlutils.lcurve(estimator, X, y, n_reps=20, score_func=accuracy_score)
plt.axhline(analitic_score, lw=2, color="black", label="bayes score")
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))

100% (9 of 9) |##########################| Elapsed Time: 0:00:00 Time:  0:00:00

<matplotlib.legend.Legend at 0x7fbdba102ac8>

estimator = SVC(gamma=100)
mlutils.lcurve(estimator, X, y, n_reps=20, score_func=accuracy_score)
plt.axhline(analitic_score, lw=2, color="black", label="bayes score")
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))

100% (9 of 9) |##########################| Elapsed Time: 0:00:00 Time:  0:00:00

<matplotlib.legend.Legend at 0x7fbdba1885c0>

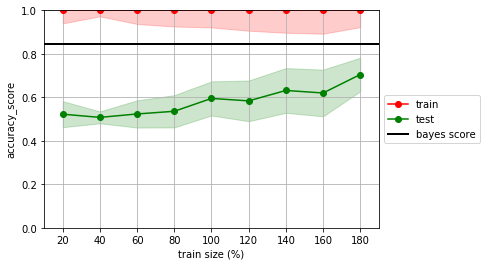
no olvides que normalmente no conocemos la frontera bayesiana, y por tanto no tenemos el bayes score

Taxonomía de problemas de machine learning

• Supervisados

  • Clasificación

  • Regresión

• No supervisados

  • Agrupamiento

  • Estimación de densidad

  • etc.

• Reinforcement learning

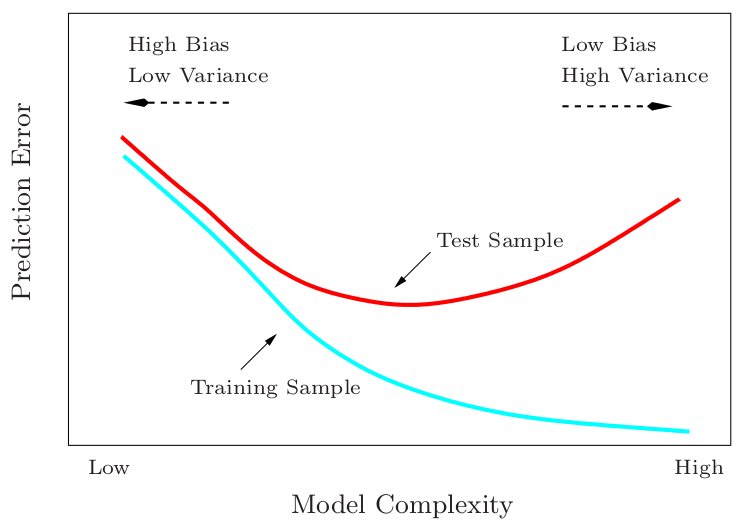
Complejidad de los modelos vs. complejidad de los datos

Image(filename='local/imgs/bvc.png', width=600)