1.3 - ML algorithm design

!wget -nc --no-cache -O init.py -q https://raw.githubusercontent.com/rramosp/2021.deeplearning/main/content/init.py
import init; init.init(force_download=False); 

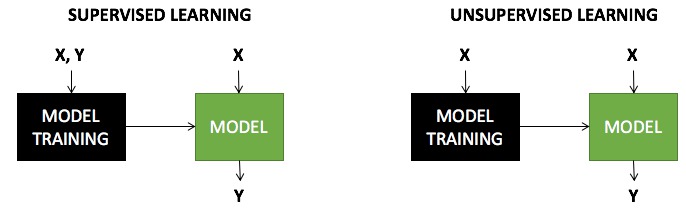
Tipos de tareas de machine learning

from IPython.display import Image
Image(filename='local/imgs/learning.jpg', width=800)

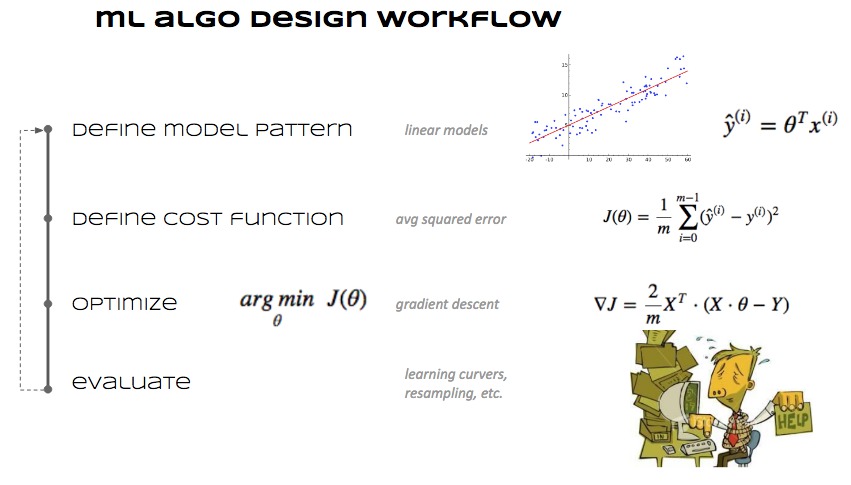
Cómo se diseña un algoritmo ML

1. Elegir de qué parámetros depende una predicción \(\rightarrow\) se define cómo es un modelo.

2. Definir una función que mida el error de la predicción.

3. Determinar qué valores de los parámetros minimizan el error de predicción.

Image(filename='local/imgs/mldesign.jpg', width=800)

Ejemplo

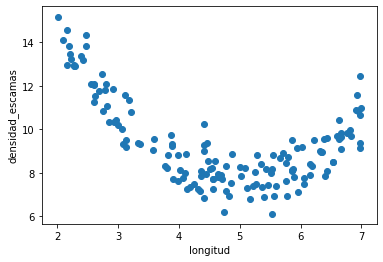
Los Trilotrópicos son insectos imaginarios que viven en las latitudes tropicales. Conocer su densidad de escamas es muy importante para poder saber qué insecticida aplicar. Pero es muy costoso contar las escamas.

Creemos que existe una relación entre la longitud y la densidad de escamas y queremos un modelo que prediga la densidad a partir de la longitud.

Esto es una tarea de regresión, ya que la predicción \(\in \mathbb{R}\)

Tenemos datos anotados (alguien contó las escamas de unos cuantos trilotrópicos) \(\rightarrow\) estamos ante una tarea de aprendizaje supervisado

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.optimize import minimize
%matplotlib inline

d = pd.read_csv("local/data/trilotropicos.csv")
print(d.shape)
plt.scatter(d.longitud, d.densidad_escamas)
plt.xlabel(d.columns[0])
plt.ylabel(d.columns[1]);

(150, 2)

1. Elegimos la forma del modelo

Entrada

• \(x^{(i)}\): longitud del trilotrópico \(i\)

Salida esperada

• \(y^{(i)}\): densidad de escamas del trilotrópico \(i\)

**Predicción ** \(\rightarrow\) decidimos que nuestro modelo tiene la siguiente forma

• \(\hat{y}^{(i)} = \theta_0 + \theta_1 x^{(i)}\)

La siguiente es una posible combinación de \(\theta_0\) y \(\theta_1\) seleccionada aleatoriamente. Ejecútalo varias veces para entender el error.

def linear_prediction(t, x):
    t0,t1 = t
    return t0 + t1*x

def plot_model(t, prediction):
    xr = np.linspace(np.min(d.longitud), np.max(d.longitud), 100)
    plt.scatter(d.longitud, d.densidad_escamas, s=40, alpha=.2, color="blue", label="")
    plt.plot(xr,prediction(t,xr), lw=2, color="black")
    plt.title("   ".join([r"$\theta_%d$=%.2f"%(i, t[i]) for i in range(len(t))]));

    p = d.iloc[np.random.randint(len(d))]
    pred = prediction(t, p.longitud)
    plt.plot([p.longitud, p.longitud], [p.densidad_escamas, pred], ls="--", color="gray", label=u"error de predicción")
    plt.scatter(p.longitud, p.densidad_escamas, s=70, alpha=.5, color="red", label="random trilobite")
    plt.scatter(p.longitud, pred, s=70, alpha=1., color="black", label=u"predicción")
    plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))

    plt.xlabel(d.columns[0])
    plt.ylabel(d.columns[1]);
    
t0 = np.random.random()*5+10
t1 = np.random.random()*4-3

plot_model([t0,t1], linear_prediction)

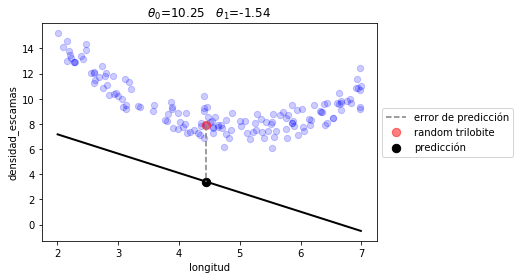
2. Definimos una medida de error

Para un dato cualquiera \((i)\) $\( \begin{align} err^{(i)} &= (\hat{y}^{(i)}-y^{(i)})^2\\ &=(\theta_0 + \theta_1 x^{(i)} - y^{(i)})^2 \end{align}\)$

Para todo el dataset

\[J(\theta_0, \theta_1) = \frac{1}{m} \sum_{i=0}^{m-1}(\theta_0 + \theta_1 x^{(i)} - y^{(i)})^2\]

si asumimos que

• \(\overline{\theta} = [\theta_0, \theta_1]\)

• \(\mathbf{x}^{(i)} = [1, x^{(i)}]\)

entonces podemos escribir de manera más compacta la expresión anterior:

\[J(\overline{\theta}) = \frac{1}{m} \sum_{i=0}^{m-1}(\overline{\theta} \dot \; \mathbf{x}^{(i)} - y^{(i)})^2\]

def J(t, x, y, prediction):
    return np.mean( (prediction(t,x)-y)**2)
    

J([t0,t1], d.longitud, d.densidad_escamas, linear_prediction)

43.30849894597834

3. Obtenemos los parámetros que minimizan el error de predicción

observa cómo usamos un algoritmo genérico de optimización

r1 = minimize(lambda t: J(t, d.longitud, d.densidad_escamas, linear_prediction), np.random.random(size=2))
r1

      fun: 2.7447662570808116
 hess_inv: array([[ 5.5736552 , -1.09197429],
       [-1.09197429,  0.23448575]])
      jac: array([1.66893005e-06, 8.22544098e-06])
  message: 'Optimization terminated successfully.'
     nfev: 40
      nit: 9
     njev: 10
   status: 0
  success: True
        x: array([12.68999875, -0.71805905])

plot_model(r1.x, linear_prediction)
print("error total %.2f"%(J(r1.x, d.longitud, d.densidad_escamas, linear_prediction)))

error total 2.74

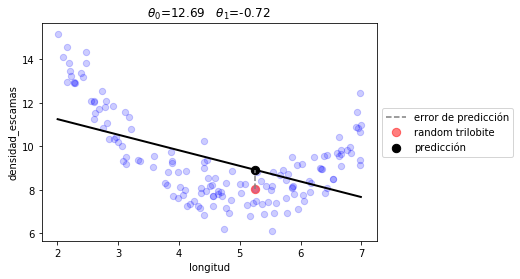
fíjate que son los mismos valores que la regresión lineal clásica

from sklearn.linear_model import LinearRegression

lr = LinearRegression()
lr.fit(d.longitud.values.reshape(-1,1), d.densidad_escamas)
t0, t1 = lr.intercept_, lr.coef_
print(t0, t1)
plot_model([t0,t1], linear_prediction)
print("error total %.2f"%(J([t0, t1], d.longitud, d.densidad_escamas, linear_prediction)))

12.689998055222224 [-0.71805908]
error total 2.74

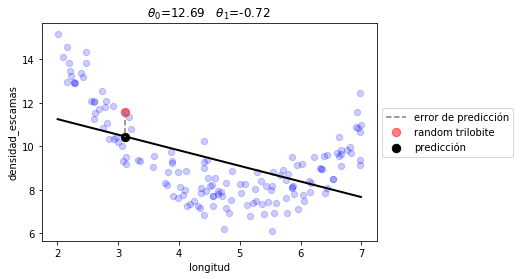
Otra forma de modelo

esta vez con tres parámetros y un término cuadrático

\[\hat{y}^{(i)} = \theta_0 + \theta_1 x^{(i)} + \theta_2 (x^{(i)})^2\]

def quad_prediction(t, x):
    t0,t1,t2 = t
    return t0 + t1*x + t2*x**2

r2 = minimize(lambda t: J(t, d.longitud, d.densidad_escamas, quad_prediction), np.random.random(size=3))
r2

      fun: 0.553307673053737
 hess_inv: array([[ 50.13033159, -22.94331661,   2.40049763],
       [-22.94331661,  10.96524782,  -1.17979412],
       [  2.40049763,  -1.17979412,   0.12978902]])
      jac: array([-5.96046448e-08, -2.53319740e-07, -1.46776438e-06])
  message: 'Optimization terminated successfully.'
     nfev: 85
      nit: 16
     njev: 17
   status: 0
  success: True
        x: array([26.75881691, -7.6105435 ,  0.757019  ])

plot_model(r2.x, quad_prediction)
print("error total %.2f"%(J(r2.x, d.longitud, d.densidad_escamas, quad_prediction)))

error total 0.55

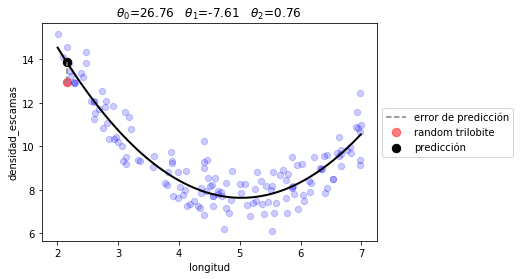
observa como indirectamente hacemos lo mismo con la regresión lineal de sklearn añadiendo explícitamente una columna con la longitud al cuadrado

lr = LinearRegression()
lr.fit(np.r_[[d.longitud.values, d.longitud.values**2]].T, d.densidad_escamas)
t0, (t1, t2) = lr.intercept_, lr.coef_
t0, t1, t2

(26.75883713364987, -7.610553466924376, 0.7570201016172378)

Tipología de algoritmos

• Generativos

• Discriminativos

Abriendo la caja negra de la optimización

EN ML, NO ES POSIBLE USAR ALGORITMOS DE OPTIMIZACIÓN TAN GENÉRICOS, debido a:

• la complejidad de los modelos.

• la participación de los datos en las expresiones.

p.ej. ¿cuántos términos tiene la siguiente expresión?

\[J(\theta_0, \theta_1) = \frac{1}{m} \sum_{i=0}^{m-1}(\theta_0 + \theta_1 x^{(i)} - y^{(i)})^2\]

1. El gradiente

para que la optimización funcione en ML es necesario calcular el gradiente de la función de pérdida (el conjunto de derivadas parciales). Observa aquí la derivación matemática del gradiente para el caso de regresión lineal (que en realidad es el más sencillo).

Usamos la notación vectorial: \(\theta = [\theta_0, \theta_1]\), \(X = [ [1, x^{(i)}] ]^m \in \mathbb{R}^{m\times 2}\) y la función de pérdida queda como:

\[J(\theta) = \text{mean}(\mathbf{X}\theta-\mathbf{y})^2\]

y el gradiente

\[\begin{split}\nabla J = \begin{bmatrix} \frac{\partial J}{\partial \theta_0}\\ \frac{\partial J}{\partial \theta_1} \end{bmatrix} = \frac{1}{m}2X^{T}\cdot(X\cdot\theta-Y)\end{split}\]

Observa ahora que cuando usamos el gradiente la minimización es mucho más eficiente (número de evaluaciones nfev) .

EN ML, SIN EL GRADIENTE LA OPTIMIZACIÓN NO ES POSIBLE

g = []

init_t = np.random.random()*40-5, np.random.random()*20-10

y = d.densidad_escamas.values
X = np.r_[[[1]*len(d), d.longitud.values]].T

def n_cost(t):
    return np.mean((X.dot(t)-y)**2)

def n_grad(t):
    return 2*X.T.dot(X.dot(t)-y)/len(X)

print("sin usar el gradiente")
r = minimize(n_cost, init_t, method="BFGS")
print(r)

print("\n usando el gradiente")
r = minimize(n_cost, init_t, method="BFGS", jac=n_grad)
print(r)

sin usar el gradiente
      fun: 2.7447662570801983
 hess_inv: array([[ 5.57513794, -1.0914388 ],
       [-1.0914388 ,  0.23472045]])
      jac: array([-2.98023224e-07, -3.57627869e-07])
  message: 'Optimization terminated successfully.'
     nfev: 24
      nit: 4
     njev: 6
   status: 0
  success: True
        x: array([12.68999713, -0.71805891])

 usando el gradiente
      fun: 2.744766257080116
 hess_inv: array([[ 5.57513616, -1.09143846],
       [-1.09143846,  0.23472038]])
      jac: array([9.11863178e-16, 4.21588690e-15])
  message: 'Optimization terminated successfully.'
     nfev: 6
      nit: 4
     njev: 6
   status: 0
  success: True
        x: array([12.68999806, -0.71805908])

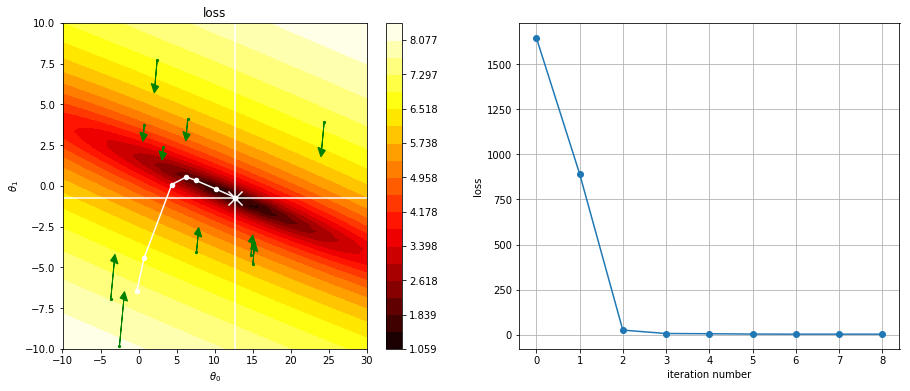
observa el mapa del coste respecto a todos los posibles valores de \(\theta_0\) y \(\theta_1\) en el caso de un modelo lineal.

en blanco los valores óptimos

2. la optimización como proceso iterativo

fíjate cómo la optimización busca un camino en el espacio de parámetros para llegar al mínimo.

import itertools
def plot_cost(cost, t0_range, t1_range, vx=None,vy=None):
    k0,k1 = 40,40

    t0 = np.linspace(t0_range[0], t0_range[1], k0)
    t1 = np.linspace(t1_range[0], t1_range[1], k1)

    p = np.zeros((k0,k1))

    for i,j in itertools.product(range(k0), range(k1)):
        p[i,j] = np.log(cost(np.r_[t0[i],t1[j]]))

    plt.contourf(t0, t1, p.T, cmap=plt.cm.hot, levels=np.linspace(np.min(p), np.max(p), 20))
    plt.ylabel(r"$\theta_1$")
    plt.xlabel(r"$\theta_0$")
    plt.title("loss")
    plt.colorbar()

    if vx is not None:
        plt.axvline(vx, color="white")
    if vy is not None:
        plt.axhline(vy, color="white")
    

g = []
loss_history = []
def log(xk):
    loss_history.append(loss(xk))
    g.append(xk)

init_t = np.random.random()*40-5, np.random.random()*20-10

loss = lambda t: J(t, d.longitud, d.densidad_escamas, linear_prediction)


r = minimize(loss, init_t, callback=log, method="BFGS")
r

      fun: 2.7447662570833065
 hess_inv: array([[ 5.55369234, -1.0871943 ],
       [-1.0871943 ,  0.23388037]])
      jac: array([ 9.53674316e-07, -4.47034836e-07])
  message: 'Optimization terminated successfully.'
     nfev: 40
      nit: 9
     njev: 10
   status: 0
  success: True
        x: array([12.69000401, -0.71806026])

plt.figure(figsize=(15,6))
plt.subplot(121)
plot_cost(loss, (-10,30), (-10,10), vx=r1.x[0], vy=r1.x[1])
g = np.r_[g]
plt.plot(g[:,0], g[:,1], color="white")
plt.scatter(g[:,0], g[:,1], color="white", s=20)
plt.scatter(g[-1,0], g[-1,1], marker="x", color="white", s=200)

# plot gradient at some points
for _ in range(10):
    t = np.random.random()*30-5, np.random.random()*20-10
    grad = n_grad(t)
    grad = grad/200
    plt.scatter(t[0],t[1], c="green", s=5)
    plt.arrow(t[0], t[1], -grad[0], -grad[1], head_width=1, head_length=0.5, fc='green', ec='green')

plt.subplot(122)
plt.plot(loss_history, marker="o")
plt.xlabel("iteration number")
plt.ylabel("loss")
plt.grid()